第 8 章 Python基础

你总是给自己设置障碍，因为你不敢。—邪不压正

8.1 Python简介

本章我们介绍Python的基础知识。在这之前，读者可能会好奇，为什么又多了一个语言？我们已经学习了R语言和SQL语言，接触了bash，在未来还要学习html语言和正则表达式。之所以学习这么多语言是因为数据工程中涵盖了多种多样的任务，针对不同的任务往往有不同的最佳工具。与其追求在一个语言中费劲完成

正如在第三章介绍的，尽管R语言非常强大，但是它毕竟不是一个通用语言，在很多任务上，效率并不高。例如，绝大多数的API都使用的是Python语法，这就极大限制了R语言的应用场景。因此，我们需要学习一门通用语言，

Python也是一门解释性语言，对于编译型语言如C/C++它更容易调试。Python的语法如R语言一般简洁易懂。Python是一个通用语言可，在生活中的方方面面都可以使用。

Python的软件库丰富，可以完成非常多其他的功能。Python可以将跨语言的程序粘合在一起，是天生的“胶水语言”，非常适合跨语言协作。

由于以上优点，Python成为当前最流行的编程语言。Python的出现大大降低了编程的门槛，程序员供给数量指数增多。

更重要的是，学习编程语言在总收益不变的情况下，边际成本是断崖式下降的，假设大家在学习R语言时候用了100%的努力，在学习Python时只用付出25%的努力，就可以快速掌握Python，但是编程能力和视野会翻倍。在未来深入学习bash时，只用付出10%的努力即可。不同的编程语言更是代表了不同的世界观，在增加技能的同时，让我们的用于更多看待世界的角度。

8.2 Python安装与Pycharm

8.2.1 安装

Python存在两个版本主要版本，Python2和Python3。Python3是针对Python2的一次大规模改进，以至于很多Python2的程序无法在Python3中运行，因此可以将两者看做是不同的语言，以避免混淆出错。

Windows用户在WSL环境中使用apt命令安装python3。

apt install python3

R用户可以通过brew或者在Gentoo prefix中的merge命令安装。

brew install python3

8.2.2 编辑器

Python有一个增强式编译环境，Ipython可用于交互式编程。还提供了Jupyter Notebook，是IPython发展而来的可以在网页上进行交互式编程的环境。它的交互性更强，可以规避掉命令行，上手容易，适合写教程。

但是，网页并不能替代编辑器，不适合写大段程序，也没有批量处理能力。如果是只是学会了Jupyter就以为自己学会了编程，到处招摇过市，会暴露自己的无知与傲慢。因此，不推荐大家将其作为编辑器使用。

8.2.3 Pycharm的安装与教育许可证

我们推荐Pycharm Professional作为Python的编辑器（下载地址），这是一款不逊色于Rstudio的编辑器，且为教育机构用户提供免费的权限。Pycharm不仅继承了语法高亮、自动补全以及版本控制等基本功能，更是集合了远程服务器编译功能，让远程调试非常便捷，这是一个Rstudio都没有的功能。同时，Pycharm也支持跨语言编辑。

安装之后请在https://www.jetbrains.com/shop/eform/students申请教育许可证。建议使用“官方文件”认证的方式。

打开Pycharm的第一步是新建项目，新建项目是要确定项目路径与编译代码的Python路径。Windows系统读者注意要使用WSL环境中的python，具体配置方法见视频。

这里对应的习惯是一个研究项目对应一个路径，其实这样的习惯在R中也应该学习。

Pycharm的窗口环境如下：

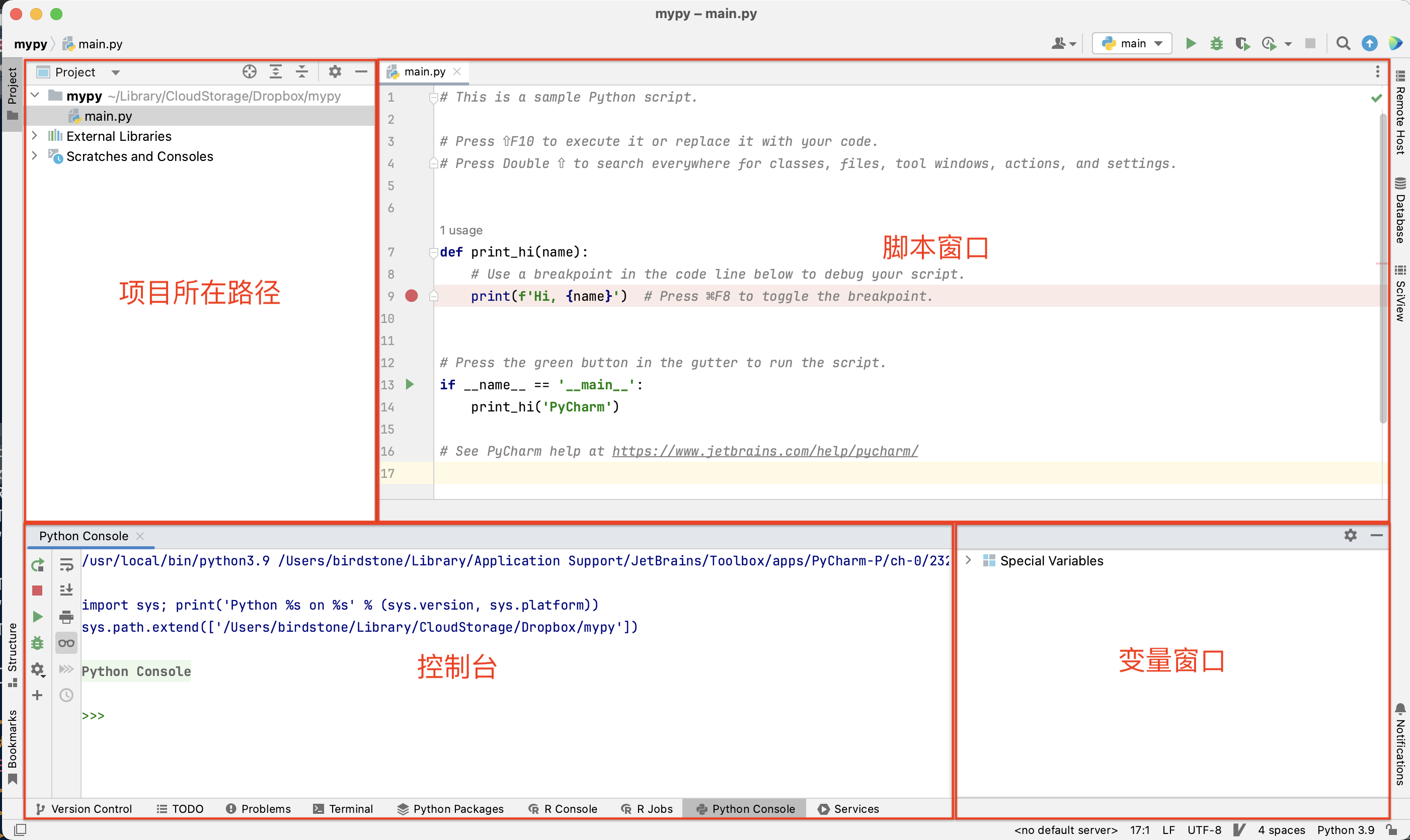
此外Rstudio也是可以兼容python的，使用reticulate::repl_python()即可将Console的编译环境变成python环境。在做一些小命令尝试的时候，可以直接在Rtudio中编程，而不需要特别转换工作环境。毕竟，任何环境的转换都是需要成本的。

8.3 变量

Python变量使用=赋值与修改，变量既可以是最基本的数据类型，也可以是复杂的数据结构，甚至是新的类实体。print函数可以将变量输出到屏幕。

a = "hello world"
print(a)

## hello world

8.4 数据类型

Python有五种数据类型：整型（精度无限的整数）、浮点型（64位高精度小数）、字符串和None。字符串引号（单引号或双引号）标注、布尔型（Ture和False）。

None是Python中一个特别的值，即不是整数也不是浮点数，属于一种独有的类型。可以代表很多含义：“空”或者“没有”，或者“无法表达”，或者“出错了”、“非法”。转换为布尔类型时，None 的赋值为“假”。

type函数可以查看的数据类型。

type(1)

## <class 'int'>

type(3.14)

## <class 'float'>

type("hello world")

## <class 'str'>

type(True)

## <class 'bool'>

type(None)

## <class 'NoneType'>

8.4.1 类型转换

int、float、str和bool函数可以转换数据类型。与R一样，不是所有类型都可以互相转换的，转换不及会报错。

8.4.2 算术运算

+-*/用于四则运算，幂运算使用两个星号，//表示整除，%为取余数。

3 + 3

## 6

3 - 3

## 0

3 * 3

## 9

3 / 2

## 1.5

3 ** 6

## 729

3 // 2

## 1

4 % 2

## 0

更复杂的运算，可以导入math模块，例如阶乘。

import math
math.factorial(10)

## 3628800

注意，在Python里面整数是高精度的，具体多少精度，取决于计算机的硬件水平。Python会自行做出判断，用计算效率损失来换取人类在编程时候的方便。这样的恰恰适合经济学家，如果能够节省人类的时间，不惜浪费计算机的时间；通过升级硬件来节约计算机的时间。

8.4.3 布尔运算

and，or，not是Python中的“与或非”运算。

True and False

## False

True or False

## True

not True

## False

<、<=、>、>=、==，!=用于数值比较，生成布尔型。

3 > 2

## True

2 != 2

## False

在Python内部，布尔型被储存成整数型的0和1，因此可进行算术运算。

2 + True

## 3

2 > False

## True

8.4.4 字符串

Python有非常强大的字符串工具库，针对单个字符串，Python开发了非常强大的属性与操作。很多操作让R用户眼睛瞪得像铜铃。例如，用加法和乘法，定义字符串的拼接与重复。

"3.14" + "15926"

## '3.1415926'

"重要的话说三次！"*3

## '重要的话说三次！重要的话说三次！重要的话说三次！'

len函数可以得到字符串的长度。

len("3.1415")

## 6

8.4.5 字符串的替换

.format函数可以实现灵活的字符串替换，例如，

"我感觉{}还需要{}，你们毕竟还是{}，你明白这意思吧？我告诉你们我是{}了，见得多了，西方哪一个{}我没有去过？你们要知道，美国的{}，比你们不知道要{}到哪里去了，我跟他{}。".format("你们新闻界","学习","too young","身经百战","国家","华莱士","高","谈笑风生")

## '我感觉你们新闻界还需要学习，你们毕竟还是too young，你明白这意思吧？我告诉你们我是身经百战了，见得多了，西方哪一个国家我没有去过？你们要知道，美国的华莱士，比你们不知道要高到哪里去了，我跟他谈笑风生。'

其中，变的部分用{}表示，.format中的参数与前面的{}一一对应。

f-string可以实现同样的功能，在数据输出时经常使用。

a = 3
b = 5
f"{a}乘以{b}等于{a*b}"

## '3乘以5等于15'

8.4.6 字符串的切片

直接用[]就可以取出字符串的子集，注意Python从0开始编号，且使用左闭右开区间，跨语言使用时别出错。

a = "hello world"
a[0],a[2:4]

## ('h', 'll')

8.4.7 标准字符串操作

Python的官方文档详尽介绍了标准库中字符串的进阶操作，推荐大家自己学一遍。我们介绍一些常用操作。

操作	作用
`.count`	统计字符出现的次数
`.startwith`	判断字符串是否由某个子串开头
`.split`	将字符串按照给定的分隔符分成列表
`.replace`	一一替换字符

seed = bin(2324)
print(seed)

## 0b100100010100

print(seed.replace('0',"奥").replace('1',"利"))

## 奥b利奥奥利奥奥奥利奥利奥奥

8.5 标准输入输出

8.5.1 标准输入

input函数可以键盘得到输入。

x = input()

标准输入默认输入数据类型为字符串，因此，当需要数字时，需要进行类型转换。标准输入使程序可与外界交互，输入信息被赋给了变量。输入可以由人给出，也可以由其它程序给出。

8.5.2 命令执行

Python默认一个命令独立成行，如果需要多个命令写在一行中，需要用分号连接不同的命令。

8.6 数据结构

把基本数据类型组合起来可以构成复杂的数据结构。Python数据结构包括列表、元组和字典。

8.6.1 列表

列表用[]表达，其中的元素用,分割。

lt = ["a","c",2]

8.6.1.1 添加

生成空列表，使用.append()方法逐步加入元素，注意每次只能加一个

lt.append(1)
print(lt)

## ['a', 'c', 2, 1]

8.6.1.2 拼接

+，+=可用于拼接列表；*用于重复。

lt + [1,2]

## ['a', 'c', 2, 1, 1, 2]

lt * 3

## ['a', 'c', 2, 1, 'a', 'c', 2, 1, 'a', 'c', 2, 1]

lt+=[1,2]
print(lt)

## ['a', 'c', 2, 1, 1, 2]

8.6.1.3 切片

与字符串一致，可以用下标取出列表特定的元素，同样是左闭右开。

lt[0:1]

## ['a']

8.6.1.4 判断

in命令可以判断元素的归属。

"b" in lt, 2 in lt

## (False, True)

8.6.1.5 删除

remove用于为删除特定元素；pop用于删除指定索引对应的元素；clear用于清空列表中所有元素，得到空列表；del删除变量。

lt.remove(1)
print(lt)

## ['a', 'c', 2, 1, 2]

lt.pop(0)

## 'a'

print(lt)

## ['c', 2, 1, 2]

lt.clear()
print(lt)

## []

8.6.2 元组

元组是一类特殊的列表，不同之处在于元组的元素不能修改。使用()生成。+与+=可以用于拼接元组，*用于重复，[]用于切片。

由于元组是不能修改的，因此只能全部删除元组。

tup1 = (1,23,4,'a')
tup2 = ("x","y")
tup = tup1 + tup2
tup[0:3]

## (1, 23, 4)

del tup

注意一个细节，("x")一个元素时，会被认为是字符串而不是元组。但是["x"]却是一个列表。

type(("x"))

## <class 'str'>

type(["x"])

## <class 'list'>

8.6.3 字典

字典是Python的经典数据结构，与JSON数据结构类似。字典用{}定义，以key:value这样的键值对定义一组词，词与词之间用,分隔。

可以通过.keys()和.values()取出字典的键和值，.items()在则可以构建迭代器。

字典的索引是通过keys实现的，是无序的，但仍可以通过对keys的索引进行元素的删除，只是不支持切片操作。

dc = {"女": 25}
dc["男"]=18
print(dc["女"])

## 25

print('男' in dc)

## True

dict和enumerate函数可以把任何序列直接生成字典。这在后续的循环迭代器构建中有妙用。

dict(enumerate("abcd"))

## {0: 'a', 1: 'b', 2: 'c', 3: 'd'}

8.6.3.1 字典的键

字典的原理要求键是不可变类型。因此，元组可以作为键，例如，

{(0, 0): "a", (0, 1): "b", (1, 0): "c"}

## {(0, 0): 'a', (0, 1): 'b', (1, 0): 'c'}

这样的数据结构适合地理数据。

8.6.3.2 删除

pop的作用为删除指定索引对应的键值对，使用方式为 dict.pop(keys)。clear与del函数的作用与对列表一致。

dc.pop("女")

## 25

print(dc)

## {'男': 18}

8.6.4 数据结构之间的转化

列表与元组之间可以无缝转换，使用tuple函数和list函数。字典中的词或者值都可以转化为列表和元组。

8.7 流程控制

8.7.1 条件判断

Python中条件判断的语法如下：

x = 10
if x % 2:
    print(f"{x}是奇数")
else:
    print(f"{x}是偶数")

## 10是偶数

上述代码构建了一个奇偶数判断器。特别要注意，Python强制要求代码缩进来表达程序的结构。如果缩进错误会直接报错。这么做的好处是可以省略掉其他语言中用于显示结构关系的标记符，例如{}。其哲学是，与其希望用户自觉缩进，不如要求强制缩进。

对于有良好编程习惯的程序员，这个约定不会带来额外的负担。

当有三重选择时，可以使用else if（或elif），搬出我们的泰山代码。

m = 100
n = 50
if m > n:
  print(m,"is lager than", n)
elif m ==n:
  print(m,"is equal to", n)
else:
  print(m,"is smaller than", n)

## 100 is lager than 50

8.7.2 循环

Python的循环结构有两种，for语句和while语句。例如，求和代码可以写成。

a = 0
n = 0
while a < 101:
  n = n + a
  a += 1
print(n)

## 5050

n = 0
for a in range(101):
  n = n + a
print(n)

## 5050

此处的range函数是生成了一个从0到100的迭代器（iterator）。在每次 for 循环时，都从迭代器中取出一个值。迭代器是一般概念，Python 中的多数多个元素组成的数据结构都可以看作迭代器。

字符串可以当成天然的迭代器，下面的写法就比R里面方便的多。

for a in "hello world":
  print(a)

## h
## e
## l
## l
## o
##  
## w
## o
## r
## l
## d

enumerate函数生成索引和迭代器，

for i, a in enumerate("hello world"):
  print(f"第{i}个字符是{a}")

## 第0个字符是h
## 第1个字符是e
## 第2个字符是l
## 第3个字符是l
## 第4个字符是o
## 第5个字符是 
## 第6个字符是w
## 第7个字符是o
## 第8个字符是r
## 第9个字符是l
## 第10个字符是d

字典也是天生的迭代器，

for k, v in {"女": 25,"男":18}.items():
  print(f"班上有{v}个{k}生")

## 班上有25个女生
## 班上有18个男生

由此看来，构造迭代器是for循环的关键。

在循环里执行continue，可以跳过本次循环进入下一步。执行break则终止循环，直接跳出循环体。这与R的用法类似。

8.8 函数与模块

Python定义函数的方式如下：

def add(x,y):
  print(f"x is {x} and y is {y}")
  return x + y  # Return values with a return statement

add(2,3)

## x is 2 and y is 3
## 5

8.8.1 批量调用

map可以将函数作用到每个元素后返回值组成的迭代器。

def squared(x):
  return x*x

list(map(squared,range(5)))

## [0, 1, 4, 9, 16]

8.8.2 无名函数

当函数只是调用一次时，可以使用无名函数的方法来定义。

list(map(lambda x:x*x,range(5)))

## [0, 1, 4, 9, 16]

8.8.3 函数文档

为了更好地解释函数的使用方法，可以在函数定义时，输入一段字符串，这样的字符串可以用help函数读出。

def squared(x):
    "计算平方的函数"
    # 具体实现省略
    return x*x

help(squared)

## Help on function squared in module __main__:
## 
## squared(x)
##     计算平方的函数

如果一大段的说明，可以使用Python多行字符串。多行字符串以三个引号开始，三个引号结束，单引号双引号皆可。

8.8.4 模块

模块是把函数等聚集起来的名字空间，由目录或者文件划定。使用import方法可以导入模块，模块都具有详实的在线帮助，可以使用help函数查看。

import math
help(math)

## Help on module math:
## 
## NAME
##     math
## 
## DESCRIPTION
##     This module provides access to the mathematical functions
##     defined by the C standard.
## 
## FUNCTIONS
##     acos(x, /)
##         Return the arc cosine (measured in radians) of x.
## 
##         The result is between 0 and pi.
## 
##     acosh(x, /)
##         Return the inverse hyperbolic cosine of x.
## 
##     asin(x, /)
##         Return the arc sine (measured in radians) of x.
## 
##         The result is between -pi/2 and pi/2.
## 
##     asinh(x, /)
##         Return the inverse hyperbolic sine of x.
## 
##     atan(x, /)
##         Return the arc tangent (measured in radians) of x.
## 
##         The result is between -pi/2 and pi/2.
## 
##     atan2(y, x, /)
##         Return the arc tangent (measured in radians) of y/x.
## 
##         Unlike atan(y/x), the signs of both x and y are considered.
## 
##     atanh(x, /)
##         Return the inverse hyperbolic tangent of x.
## 
##     cbrt(x, /)
##         Return the cube root of x.
## 
##     ceil(x, /)
##         Return the ceiling of x as an Integral.
## 
##         This is the smallest integer >= x.
## 
##     comb(n, k, /)
##         Number of ways to choose k items from n items without repetition and without order.
## 
##         Evaluates to n! / (k! * (n - k)!) when k <= n and evaluates
##         to zero when k > n.
## 
##         Also called the binomial coefficient because it is equivalent
##         to the coefficient of k-th term in polynomial expansion of the
##         expression (1 + x)**n.
## 
##         Raises TypeError if either of the arguments are not integers.
##         Raises ValueError if either of the arguments are negative.
## 
##     copysign(x, y, /)
##         Return a float with the magnitude (absolute value) of x but the sign of y.
## 
##         On platforms that support signed zeros, copysign(1.0, -0.0)
##         returns -1.0.
## 
##     cos(x, /)
##         Return the cosine of x (measured in radians).
## 
##     cosh(x, /)
##         Return the hyperbolic cosine of x.
## 
##     degrees(x, /)
##         Convert angle x from radians to degrees.
## 
##     dist(p, q, /)
##         Return the Euclidean distance between two points p and q.
## 
##         The points should be specified as sequences (or iterables) of
##         coordinates.  Both inputs must have the same dimension.
## 
##         Roughly equivalent to:
##             sqrt(sum((px - qx) ** 2.0 for px, qx in zip(p, q)))
## 
##     erf(x, /)
##         Error function at x.
## 
##     erfc(x, /)
##         Complementary error function at x.
## 
##     exp(x, /)
##         Return e raised to the power of x.
## 
##     exp2(x, /)
##         Return 2 raised to the power of x.
## 
##     expm1(x, /)
##         Return exp(x)-1.
## 
##         This function avoids the loss of precision involved in the direct evaluation of exp(x)-1 for small x.
## 
##     fabs(x, /)
##         Return the absolute value of the float x.
## 
##     factorial(n, /)
##         Find n!.
## 
##         Raise a ValueError if x is negative or non-integral.
## 
##     floor(x, /)
##         Return the floor of x as an Integral.
## 
##         This is the largest integer <= x.
## 
##     fmod(x, y, /)
##         Return fmod(x, y), according to platform C.
## 
##         x % y may differ.
## 
##     frexp(x, /)
##         Return the mantissa and exponent of x, as pair (m, e).
## 
##         m is a float and e is an int, such that x = m * 2.**e.
##         If x is 0, m and e are both 0.  Else 0.5 <= abs(m) < 1.0.
## 
##     fsum(seq, /)
##         Return an accurate floating point sum of values in the iterable seq.
## 
##         Assumes IEEE-754 floating point arithmetic.
## 
##     gamma(x, /)
##         Gamma function at x.
## 
##     gcd(*integers)
##         Greatest Common Divisor.
## 
##     hypot(...)
##         hypot(*coordinates) -> value
## 
##         Multidimensional Euclidean distance from the origin to a point.
## 
##         Roughly equivalent to:
##             sqrt(sum(x**2 for x in coordinates))
## 
##         For a two dimensional point (x, y), gives the hypotenuse
##         using the Pythagorean theorem:  sqrt(x*x + y*y).
## 
##         For example, the hypotenuse of a 3/4/5 right triangle is:
## 
##             >>> hypot(3.0, 4.0)
##             5.0
## 
##     isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
##         Determine whether two floating point numbers are close in value.
## 
##           rel_tol
##             maximum difference for being considered "close", relative to the
##             magnitude of the input values
##           abs_tol
##             maximum difference for being considered "close", regardless of the
##             magnitude of the input values
## 
##         Return True if a is close in value to b, and False otherwise.
## 
##         For the values to be considered close, the difference between them
##         must be smaller than at least one of the tolerances.
## 
##         -inf, inf and NaN behave similarly to the IEEE 754 Standard.  That
##         is, NaN is not close to anything, even itself.  inf and -inf are
##         only close to themselves.
## 
##     isfinite(x, /)
##         Return True if x is neither an infinity nor a NaN, and False otherwise.
## 
##     isinf(x, /)
##         Return True if x is a positive or negative infinity, and False otherwise.
## 
##     isnan(x, /)
##         Return True if x is a NaN (not a number), and False otherwise.
## 
##     isqrt(n, /)
##         Return the integer part of the square root of the input.
## 
##     lcm(*integers)
##         Least Common Multiple.
## 
##     ldexp(x, i, /)
##         Return x * (2**i).
## 
##         This is essentially the inverse of frexp().
## 
##     lgamma(x, /)
##         Natural logarithm of absolute value of Gamma function at x.
## 
##     log(...)
##         log(x, [base=math.e])
##         Return the logarithm of x to the given base.
## 
##         If the base is not specified, returns the natural logarithm (base e) of x.
## 
##     log10(x, /)
##         Return the base 10 logarithm of x.
## 
##     log1p(x, /)
##         Return the natural logarithm of 1+x (base e).
## 
##         The result is computed in a way which is accurate for x near zero.
## 
##     log2(x, /)
##         Return the base 2 logarithm of x.
## 
##     modf(x, /)
##         Return the fractional and integer parts of x.
## 
##         Both results carry the sign of x and are floats.
## 
##     nextafter(x, y, /, *, steps=None)
##         Return the floating-point value the given number of steps after x towards y.
## 
##         If steps is not specified or is None, it defaults to 1.
## 
##         Raises a TypeError, if x or y is not a double, or if steps is not an integer.
##         Raises ValueError if steps is negative.
## 
##     perm(n, k=None, /)
##         Number of ways to choose k items from n items without repetition and with order.
## 
##         Evaluates to n! / (n - k)! when k <= n and evaluates
##         to zero when k > n.
## 
##         If k is not specified or is None, then k defaults to n
##         and the function returns n!.
## 
##         Raises TypeError if either of the arguments are not integers.
##         Raises ValueError if either of the arguments are negative.
## 
##     pow(x, y, /)
##         Return x**y (x to the power of y).
## 
##     prod(iterable, /, *, start=1)
##         Calculate the product of all the elements in the input iterable.
## 
##         The default start value for the product is 1.
## 
##         When the iterable is empty, return the start value.  This function is
##         intended specifically for use with numeric values and may reject
##         non-numeric types.
## 
##     radians(x, /)
##         Convert angle x from degrees to radians.
## 
##     remainder(x, y, /)
##         Difference between x and the closest integer multiple of y.
## 
##         Return x - n*y where n*y is the closest integer multiple of y.
##         In the case where x is exactly halfway between two multiples of
##         y, the nearest even value of n is used. The result is always exact.
## 
##     sin(x, /)
##         Return the sine of x (measured in radians).
## 
##     sinh(x, /)
##         Return the hyperbolic sine of x.
## 
##     sqrt(x, /)
##         Return the square root of x.
## 
##     sumprod(p, q, /)
##         Return the sum of products of values from two iterables p and q.
## 
##         Roughly equivalent to:
## 
##             sum(itertools.starmap(operator.mul, zip(p, q, strict=True)))
## 
##         For float and mixed int/float inputs, the intermediate products
##         and sums are computed with extended precision.
## 
##     tan(x, /)
##         Return the tangent of x (measured in radians).
## 
##     tanh(x, /)
##         Return the hyperbolic tangent of x.
## 
##     trunc(x, /)
##         Truncates the Real x to the nearest Integral toward 0.
## 
##         Uses the __trunc__ magic method.
## 
##     ulp(x, /)
##         Return the value of the least significant bit of the float x.
## 
## DATA
##     e = 2.718281828459045
##     inf = inf
##     nan = nan
##     pi = 3.141592653589793
##     tau = 6.283185307179586
## 
## FILE
##     /usr/local/Cellar/python@3.12/3.12.1/Frameworks/Python.framework/Versions/3.12/lib/python3.12/lib-dynload/math.cpython-312-darwin.so

当模块中的内容很多时，会被安排在不同层次的名字空间中，可以使用from来简化调用，as可以指定模块的别名。

import os
from os.path import abspath
from os.path import abspath as absp

8.9 数据读写与文件操作

之前我们介绍了通过input从键盘输入和print输出到屏幕。除此之外，还可以直接从文件读入和输出到文件。Python内置了file类，来完成文件操作。

8.9.1 读入文件

open函数用于打开文件，创建一个file对象，第一个参数是文件名，第二参数为打开模式，默认值r表示只读，w表示写出，a表示添加。

open打开文件之后，用迭代器逐行读取。

for l in open("log.txt"):
  print(l,end = "") # 读入的字符串带有换行符，与print 叠加会有空行，end参数表示去掉空行。

## This is a record of my progress in learning Python
## Day 1: Introduction

8.9.2 写出文件

open以写模式打开，可以输出到文件。

f = open("log.txt", "w")
f.write("Day 2: Basics\n")

## 14

f.write("Day 3: Numpy\n")

## 13

f.close()

注意文件写出完成后，需要关闭文件，否则会一直建立关联，占用资源。

写出模式下，之前的内容会会被覆盖，如果希望添加到已有内容中，需要使用添加模式。

f = open("log.txt", "a")
f.write("Day 4: Scrapy\n")

## 14

f.close()

8.9.3 with关键字

使用with关键字系统会自动调用f.close方法。

with open("log.txt","r") as f:
  for l in f.readlines():
    print(l,end = "")

## Day 2: Basics
## Day 3: Numpy
## Day 4: Scrapy

readlines方法是逐行读入文件，是一个天然的迭代器。

with open("log.txt","a") as f:
  f.write("Day 5: Machine Learning\n")

## 24

8.10 os模块

os提供了帮你执行文件处理操作的方法，比如重命名和删除文件。

方法	作用
`remove`	删除文件
`rename`	重名命文件
`mkdir`	创建新目录
`chdir`	改变当前目录
`getcwd`	查看当前目录
`rmdir`	删除目录

8.11 Python的环境配置

笼统地说，Python环境指的是“解释器（即python本身）与其使用模块的整体”。如下图所示，有两种方案来管理python的环境，一种是只针对python内部的pip管理器方案，另一种是跨语言的环境整合方案。注意，此时的环境管理指的是拥有管理员权限的管理。

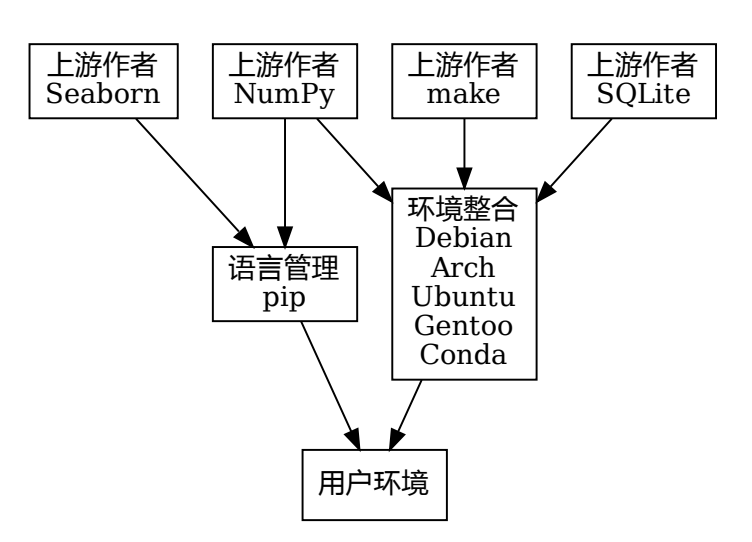
pip是python自带的语言管理工具，只适合早期试验个别最新的python软件，长期维护性差，而且只适用于python。pip会和系统的库发生冲突，出现玄学问题。

更严重的是，pip没有经过第三方检测，意味着无条件相信上游软件作者，没有办法保障安全，不确定是否会被恶意植入病毒代码，在不知不觉中隐私信息被窃取，或者电脑被他人操纵。这样的重大安全事故，历史上已经发生过多次。

环境整合方案则是需要经过跨语言整合测试的方案，对应多种软件的稳定版本。会有负责安全、兼容和性能的团队，以及大量使用相同环境的用户反馈问题。环境整合方案意味着我们要信任环境整合的第三方。

环境整合方案有两种模式：Debian/Arch/Gentoo志愿者模式与Ubuntu/Conda公司免费模式。前者的开发团队由没有利益关系的、兴趣一致的人们通过git共同开发，没有人能够强制整个项目的走向，集体决策，是一种民主模式。后者则是利用免费服务吸引用户，构建潜在的客户池或者暗藏广告来改造用户，产品总是服务于公司的盈利或扩大影响的战略，代码是有雇员生产的，雇员的总体规模肯定远小于志愿者模式。

我们不推荐使用公司模式，Ubuntu的代码95%直接来自Debian，且公司曾经定制广告；Conda的依赖关系的计算效率极低，但在公司层面花费大量的外宣经费进行推广，所以互联网上可以看到大量的技术博主推广conda，看上去仿佛conda是被所有人喜欢的，这是NGO的一种宣传策略。所以，非常不推荐使用conda。

上面的场景对应的是自己拥有root权限，可以维护自己的主机或者一个服务器的整体环境。还有一种情形是自己只有普通用户权限，此时推荐使用Gentoo Prefix进行用户态管理。Gentoo Prefix由续本达召集管理，有问题可以直接物理上找到召集人，还是更放心的。

值得一提的是，对于macOS用户,Homebrew提供了志愿者模式的环境整合方案，本书目前推荐Homebrew模式，但是brew中的依赖经常滞后，存在一定的局限性；Gentoo Prefix也为macOS开发了一套环境整合方案，更适用于科学计算，但是Gentoo Prefix的安装与使用，会遇到一些玄学问题，作者自己也没有完全搞定，如果全部搞定之后，会将教材替换成Gentoo Prefix模式。

总结起来就是，自己的机器用Debian，工具安装用apt；他人的机器用Gentoo Prefix，工具安装用emerge。